1.0. INTRODUCTION

The media extensions to the Intel Architecture (IA) instruction set include single-instruction, multiple-data (SIMD) instructions. This application note presents examples of code that exploit these instructions. Specifically, it shows how to use the MMX^TM technology PMADDWD instruction to significantly speed up computation of 16-bit Finite Impulse Response (FIR) digital filters. The PMADDWD instruction multiplies four pairs of 16-bit numbers and produces partial sums of the results. The PMADDWD instruction can be scheduled every clock cycle (with a three-cycle latency). The results are accumulated with 32-bit precision and converted to 16 bits after computation.

2.0. 16-BIT REAL FIR FILTER

Where M is the length of the filter and N is the length of the input and output sequences (0£n<N). N is typically much larger than M. Note that c0, c1, ¼,and cM are the response of the filter to a unit impulse—this sample is finite in length, hence the name. This equation can be used to compute the output sequence. Given an input sequence of length N and a filter of length M, the computation will include N*M multiply-accumulate operations. The numbers c0, c1, ¼, and cM are commonly referred to as the coefficients or taps of the filter. Note that the computation of the first M-1 output element requires access to elements before the start of the input sequence (x(n) for n£0). These elements are taken to be zero.

2.1. MMX™ Technology Routine Overview

If the filter data is stored in memory in reverse order, the calculation of each output data component becomes essentially a vector dot-product calculation:

For 16-bit data, vector dot-product calculations are efficiently implemented using MMX technology instructions by loading and processing four data elements at a time, using the PMADDWD instruction. The main loop of this implementation appears in Figure 1.

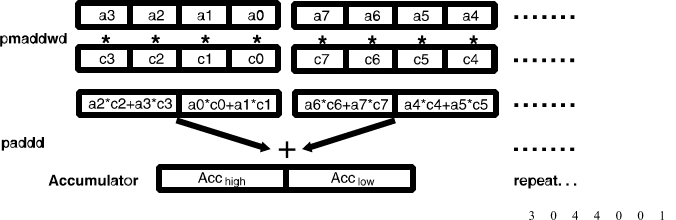
Figure 1. Main Loop of 16-Bit Vector Dot-Product Using MMX™ Technology Instructions

The MMX technology PMADDWD instruction is used on four elements from each vector. The results are two 32-bit numbers: the sum of the first two products and the sum of the second two products. These are accumulated into an MMX technology register using PADDD. This operation is repeated on the next four elements until all of the elements have been multiplied.

At the end of this loop the accumulator register contains two (doubleword) partial sums. The actual result of the vector dot-product is the sum of these partial sums. That is, the low and high doublewords must be added together. There are several methods to do this. (For more details, see Section 2.3.2, “Summing and Packing Results” of this document and AP-AP-557, “Using MMX^TM Technology Instructions to Compute a 16-Bit Vector Dot Product” (Order Number 243042).

This loop forms the basis for the MMX technology optimized code implementation of a 16-bit real FIR filter. However, simply wrapping an outer loop around a vector dot-product routine does not yield the maximum possible performance. There are several performance considerations which should also be taken into account. Depending on the filter and input data, a shift instruction may be necessary after the PADDD instruction to prevent overflow.

2.2. MMX™ Technology Code Performance Considerations

The following sections describe two performance considerations that were taken into account when implementing this digital FIR filter:

• Data Alignment
• Loop Unrolling

2.2.1. Data Alignment

In the case of an FIR filter, the relative alignment of the input and filter elements changes from one vector dot-product calculation to the next (see Figure 2.)

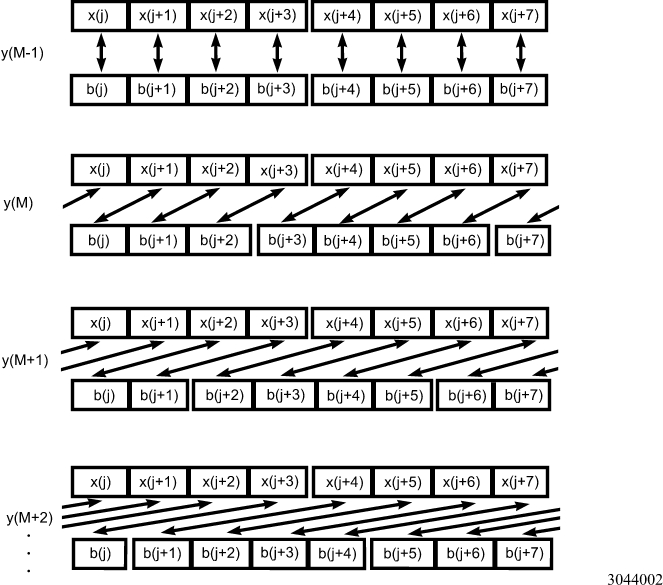
Figure 2. Relative Alignment of 16-Bit Input and Filter Data

Figure 2 shows the relative alignment of the groups of four elements in the input and filter data. (The arrows show elements which are multiplied together.) The relative alignment changes by one element (2 bytes) for each vector dot-product calculation. This implies that in three out of four vector dot-product calculations, all accesses to one of the vectors will be misaligned (8-byte data accesses which are not on 8-byte-aligned addresses).

Because each misaligned data access has a three-clock penalty, the performance will be severely impaired unless the misaligned accesses can be avoided. One way to avoid misaligned data accesses is to have four copies of the filter data, each one with a different alignment relative to an 8-byte boundary. Because the filter data is usually constant and much smaller in size than the input data, this solution does not have a significant overhead cost in memory space or speed. For each vector dot-product, a different copy of the filter is used to ensure that all data accesses are to aligned addresses (see Figures 3 and 4.)

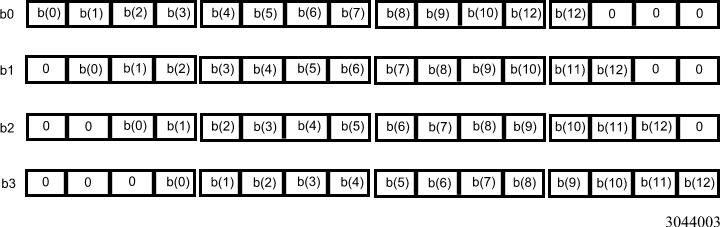
Figure 3. Multiple Copies of Filter Data

Figure 4. Using Multiple Copies of Filter Data to Avoid Misaligned Accesses

Figure 3 shows the structure of the four copies of the filter data (a filter length of 13 is used as an example—this can be easily adopted for other filter lengths). Note that the copies are padded with zeros at the beginning and/or at the end.

Figure 4 shows the use of the copies to avoid misaligned accesses. When calculating each element of the result, the vector dot-product calculation is performed using the correct copy to ensure that all data accesses are aligned to 8-byte boundaries.

2.2.2. Loop Unrolling

When writing an efficient 16-bit FIR filter implementation using MMX technology, careful loop unrolling helps achieve maximum parallelism. If the filter is relatively short (not much longer than 64 coefficients), the vector dot-product code is short enough to be entirely unrolled. This exposes more scheduling opportunities that can be taken advantage of to avoid stalls and improve instruction pairing. If the filter is shorter, (about 32 coefficients) it is recommended that you also unroll the outer loop twice, thus calculating two vector dot-products in each iteration. For even shorter filters (about 16 coefficients) the outer loop should be unrolled four times. Note that these are rough guidelines; other factors besides the filter length should be taken into account when deciding how many times to unroll the loop.

There are several benefits to unrolling the outer loop twice:

• Two sets of partial sums can be combined and added, which is faster than adding the partial sums for each result separately. For additional information, see Section 2.4.2, “Summing and Packing Results.”
• Because the same input data is used twice (once with each filter copy), it can be loaded from memory to a register once and copied to other registers three times, instead of being loaded it four times from memory. This reduces the percentage of MMX technology instructions which access memory below 50 percent, which increases potential pairing.
• More opportunities for instruction scheduling are exposed, because two independent instruction streams are available.

There are several benefits to unrolling the outer loop four times (in addition to the benefits achieved by unrolling it twice):

• The overhead of selecting the correct filter copy is eliminated, because each of the four filter copies is used once inside the loop.
• Some additional opportunities for instruction scheduling are exposed, though most are exposed by unrolling twice. For additional information, see Section 2.4.1, “Register Allocation.”

Of course, there is also a disadvantage to aggressive loop unrolling—code size increases and the instruction cache hit rate is reduced. For this reason less loop unrolling should be performed for longer filters, so as not to increase the code size too much.

In this document, a short filter is assumed (a 13-tap filter is used in the code listing) so the outer loop is unrolled four times.

2.3. MMX™ Technology Code Details

The examples shown in this section are 16-bit real FIR filters with 13 taps, running on a long sequence of input data. The filter data is kept in four copies to avoid misaligned accesses and the main loop calculates four elements of the output data.

2.3.1. Multiply-Accumulate Sequence

Because the same input data is used with different filter copies, the input data can be loaded once from memory and copied. This is important because otherwise the number of memory accesses would limit performance. There are three instructions (MOVQ, PMADDWD, PADDD) in a multiply-accumulate sequence. This enables a throughput of one multiply-multiply-accumulate (on four 16-bit operand pairs) per 1.5 clocks. If both operands of each sequence are loaded from memory, the two memory accesses limit bandwidth to one multiply-accumulate per two clocks (because only one MMX technology instruction which accesses memory can be executed per cycle).

A sequence of code which reuses an operand to do two multiply-accumulate operations with three memory accesses appears in Example 1.

movq 	mmA, x[j+n-M+1]movq 	mmB, mmApmaddwd	mmA, b0[j]pmaddwd	mmB, b1[j]padd	Acc1, mmApadd	Acc2, mmB

The first multiply-accumulate sequence in the vector dot-product calculation initializes the accumulator registers instead of accumulating. So the code for the first sequence is slightly different:

movq	Acc1, x[j]movq	Acc2, Acc1pmaddwd	Acc1, b0[j+n]pmaddwd	Acc2, b1[j+n]

2.3.2. Alternate Multiply-Accumulate Sequence

An alternate multiply-accumulate sequence appears in Example 3.

movq	mmA, x[j+n-M+1]movq	mmB, b0[j]pmaddwd	mmB, mmApmaddwd	mmA, b1[j]padd	Acc1, mmApadd	Acc2, mmB

This sequence might yield better performance on Pentium^(R) Pro processors, because it generates fewer micro-operations. This is because it has a register-register PMADDWD (1 micro-operation) and a register-memory MOVQ (1 micro-operation) instead of a register-memory PMADDWD (2 micro-operations) and a register-register MOVQ (1 micro-operation.)

2.3.3. Summing and Packing Results

After the four multiply-accumulate sequences, each accumulator contains a packed doubleword, each half of which contains half of the result in 32-bit precision. These halves must be summed together and packed to 16-bit precision before storing.

This operation is more efficient when performed on two results. To sum and pack one accumulator, the following code sequence is used:

movq	mmA, Accpsrlq	Acc, 32paddd	Acc, mmApackssdw	Acc, Accmovd	[result], Acc

To sum and pack two accumulators together, the following code sequence is used:

movq	mmA, Acc1punpckhdq	mmA, Acc2punpckldq	Acc1, Acc2paddd	Acc1, mmApackssdw	Acc1, Acc1movd	[result+4], Acc

The second operand for the PACKSSDW instruction can be the contents of any register. The result has relevant data in the low 32 bits and can be stored to memory with a MOVD instruction. If it is possible to calculate results for four accumulators in parallel, all can be packed with one PACKSSDW instruction and the result for all four can be stored with one MOVQ instruction. This sequence is the one used in the code listing at the end of this application note.

2.3.4. Combining Writes into Quadwords

In cases where the output buffer is not in the cache, it may help performance to write into this buffer eight bytes at a time, rather than four. This can be accomplished with the alternate code sequences presented in Examples 6 and 7.

movq	mmA, Acc1punpckhdq	mmA, Acc2punpckldq	Acc1, Acc2paddd	Acc1, mmAmovq	[temp], Acc1

movq	mmA, Acc1punpckhdq	mmA, Acc2punpckldq	Acc1, Acc2paddd	Acc1, mmAmovq	mmC, [temp]packssdw	mmC, Acc1movq	 [result], Acc

2.3.5. Register Allocation

The inner loop is entirely unrolled, so four packed word multiply-accumulate sequences are sufficient (more would be required if the filter was longer than 13 taps). The outer loop was unrolled four times. Because the multiply-accumulate sequences perform operations from two different iterations of the outer loop, there are two instruction streams. Each instruction stream requires at least four registers (see Example 1).

Two alternatives were considered for register allocation:

• Allocating four distinct registers to each instruction stream. In this case, the reordering and pairing within each instruction stream is relatively limited, but the two streams have no interdependencies, and the mixing of instructions from the two streams is limited only by available resources.
• Using all eight registers within each instruction stream. This enables more reordering and pairing of instructions within each stream. The two streams must be scheduled in series, but some limited mixing may be possible between the streams around the boundaries between them.

After checking the performance possible with both approaches, it was decided to use the second approach, because it enabled more efficient instruction scheduling.

2.3.6. Instruction Flow Diagram

The instruction flow diagram for each instruction stream appears in Figure 5.

3.0. PERFORMANCE GAINS

This section describes the performance improvement as compared with traditional scalar code. MMX technology optimized code provides, approximately, a 500 percent performance gain. The results presented here assume the input and output buffers are in the L1 cache and aligned to eight bytes—gains are reduced if there are cache misses or misaligned accesses. It is also assumed that the input data sequence is long enough for the loop performance to dominate, so that the effect of the pre- and post-loop overhead is negligible.

3.1. Performance of Scalar Code

Because floating-point multiplication is significantly faster than scalar integer multiplication, the fastest scalar implementation is in floating-point. To make a comparison, the performance estimate is for code where the inner loop is entirely unrolled and the outer loop has been unrolled four times. A well-optimized floating-point implementation should be able to issue one multiplication, add, or load per clock, to achieve a throughput of one multiply-accumulate per three clocks. Counting additional overhead, the scalar loop should require at least 160 clocks to execute per iteration.

The implementation in this application note assumes that all input and output data is in floating-point format. If conversions must be performed to or from integer, the performance of the scalar code will not be as good.

3.2. Performance of MMX™ Technology Code

The outer loop executes in 31 clocks, which is over five times faster than the scalar (floating-point) loop. For input vectors much longer than 16 elements, the total performance improvement for the FIR filter calculation should approach that of the loop (five times the original), assuming all data is in the cache and that both vectors are aligned to eight bytes. If there is significant overhead for converting the data from integer to floating point, the speedup compared to scalar code will be higher. This speedup is mostly attributable to the MMX technology instructions which perform operations on multiple data elements and can be paired, unlike the floating-point instructions.

In this code one operand is reused for two operations. The peak rate using MMX technology instructions, in this case, is eight 16-bit multiply-accumulate operations per three clocks. Peak rate using floating-point instructions is one multiply-accumulate operation per three clocks. The peak speedup is 800 percent, but the actual speedup is much lower because the filter is short and the various sources of overhead are significant.

4.0. 16-BIT REAL FIR FUNCTION: CODE LISTING

INCLUDE iammx.inc	 TITLE firmmx	.486Pinclude listing.inc.model FLATPUBLIC _firmmx_DATA SEGMENT_DATA ENDS_TEXT SEGMENT_s1Ptr$  = 16_s2Ptr$  = 20_size$   = 24_resPtr$ = 28;F;Purpose :    Applies a 16-bit real FIR filter to an input sequence.;               This routine assumes the filter length is 13, and that;               the filter data is in four copies and padded with zeros;               (see Note 2 below).;Context:;       void ;       firmmx (;               short	*src1,;               short	*src2,;               int		size,;               short	*result) ;;Returns:;Parameters:;           src1     Pointer to the input vector src1.;           src2     Pointer to the filter array src2.;           vecsize  The size of the input vector (in words).;           result   Pointer to the result.;Notes:;       1.  For best performance, align input and output vectors to 8 		       bytes.;;       2.  The filter data is a vector of four 16-word vectors.;           Each array is a copy of the filter data which is padded with;           zeros and aligned differently. The purpose of this is to avoid;           misaligned accesses to the filter data. The data format is:;           ;  f0:      +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+;  src2[0]  |f00|f01|f02|f03|f04|f05|f06|f07|f08|f09|f10|f11|f12| 0 | 0 | 0 |;           +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+;;  f1:      +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+;  src2[32] | 0 |f00|f01|f02|f03|f04|f05|f06|f07|f08|f09|f10|f11|f12| 0 | 0 |;           +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+;;  f2:      +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+;  src2[64] | 0 | 0 |f00|f01|f02|f03|f04|f05|f06|f07|f08|f09|f10|f11|f12| 0 |;           +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+;;  f3:      +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+;  src2[96] | 0 | 0 | 0 |f00|f01|f02|f03|f04|f05|f06|f07|f08|f09|f10|f11|f12|;           +---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+;;F_firmmx PROC NEAR    push        ebx    push        esi    push        edi;Load arguments    mov         edi, _s1Ptr$[esp]  ; src1 pointer    mov         ebx, _s2Ptr$[esp]  ; src2 pointer    mov         ecx, _size$[esp]   ; size of input array (src1)    mov         edx, _resPtr$[esp] ; pointer to the result; Set up for loop: edi and edx start pointing to the end of the input and; output arrays. ecx is equal to -2*size and is incremented by 8 each; iteration until it reaches 0.; [edi+ecx] accesses the input array, [edx+ecx] accesses the output array.    sal         ecx, 1             ; ecx = size * 2    add         edx, ecx           ; set edx, edi to point to the    add         edi, ecx           ; end of their arrays    neg         ecx                ; ecx = size * (-2);.align 16;Loop structure:; Each iteration of this loop calculates four output values.; Four vector dot-products are performed between the input data and the; filter (each one using a different copy of the filter data to avoid; misaligned data accesses).; There are two instruction streams: one calculates the first two results; (using filter copies f0 and f1) and the other calculates the last two; results (using filter copies f2 and f3).; Each instruction stream contains four multiply-accumulate sections and; one combine/pack section. Each multiply-accumulate section performs; two PMADDWD operations (one between the input data and each of the two; filter copies), and accumulates the results with two PADDD instructions.; (The first MACC section in each stream does PMADDWD directly to the; accumulator registers and does not need PADDDs to accumulate.); The MMX technology registers used in each stream:;Stream one:;   Accumulators:   MM6, MM7 (also MACC0);   MACC2:          MM0, MM1;   MACC3:          MM2, MM3;   MACC4:          MM4, MM5;   Combine/pack:   MM1;Stream two:;   Accumulators:   MM4, MM5 (also MACC0);   MACC2:          MM2, MM3;   MACC3:          MM0, MM1;   MACC4:          MM6, MM7;   Combine/pack:   MM3; Each instruction inside the loop is commented by which stream it belongs to; (0/1 or 2/3) and which section (MACC0, MACC1, MACC2, MACC3, CMPCK).; This is useful to keep track of the instructions, because the instructions; inside the loop have been extensively reordered to improve performance.; The four results are referred to as out0, out1, out2, out3.; The input vector is referred to as 'in[]'.;Scheduling:; Software pipelining was used to facilitate instruction scheduling - some; operations from the end of the previous iteration are performed with the; instructions of this iteration. The first four results are calculated; before the loop to 'prime the pump'.; NOTE: this means that there must be at least eight elements in the output;       vector for this routine to function correctly.; The instructions before and after the loop were not reordered because they; are only executed once per function call, so the performance gain is nil.;Pre-loop:; Start calculating first four results. This is a degenerate loop iteration.; Because the first 12 input data elements are actually zero, only the last; quadword needs to be processed. (MACC3, CMPCK); Some registers are initialized to zero so the software-pipelined; instructions at the start of the loop work correctly.    movq        MM6, [edi+ecx+24]  ; MACC3(0/1): load in[n+15:n+12]    movq        MM7, MM6           ; MACC3(0/1): copy in[n+15:n+12]    pmaddwd     MM6, [ebx+24]      ; MACC3(0/1): in[n+15:n+12] * f0[15:12]    pmaddwd     MM7, [ebx+56]      ; MACC3(0/1): in[n+15:n+12] * f1[15:12]    movq        MM1, MM6           ; CMPCK(0/1): copy out0    punpckhdq   MM1, MM7           ; CMPCK(0/1): unpack high out0,out1    punpckldq   MM6, MM7           ; CMPCK(0/1): unpack low out0,out1    paddd       MM6, MM1           ; CMPCK(0/1): add high+low out0,out1    packssdw    MM6, MM6           ; CMPCK(0/1): pack 32->16 out0, out1    movd        [edx+ecx], MM6     ; CMPCK(0/1): store out0, out1    movq        MM4, [edi+ecx+24]  ; MACC3(2/3): load in[n+15:n+12]    movq        MM5, MM4           ; MACC3(2/3): copy in[n+15:n+12]    pmaddwd     MM4, [ebx+88]      ; MACC3(2/3): in[n+15:n+12] * f2[15:12]    pmaddwd     MM5, [ebx+120]     ; MACC3(2/3): in[n+15:n+12] * f3[15:12]    pxor		MM1, MM1           ; MACC2(2/3): prepare out3 accumulation    pxor		MM6, MM6           ; MACC3(2/3): prepare out2 accumulation    pxor		MM7, MM7           ; MACC3(2/3): prepare out3 accumulation    add         ecx, 8             ; n += 4; Start the loop from the next four results. (n=4); Instructions marked PREV belong to the previous loop iteration.; (software pipelining).NextInputs:    paddd       MM5, MM1           ; MACC2(2/3): accumulate out3    paddd       MM4, MM6           ; MACC3(2/3): accumulate out2    paddd       MM5, MM7           ; MACC3(2/3)PREV: accumulate out3    movq        MM3, MM4           ; CMPCK(2/3)PREV: copy out2    movq        MM6, [edi+ecx]     ; MACC0(0/1): load in[n+3:n]    punpckhdq   MM3, MM5           ; CMPCK(2/3)PREV: unpack high out2,out3    movq        MM0, [edi+ecx+8]   ; MACC1(0/1): load in[n+7:n+4]    movq        MM7, MM6           ; MACC0(0/1): copy in[n+3:n]    pmaddwd     MM6, [ebx]         ; MACC0(0/1): in[n+3:n] * f0[3:0]    movq        MM1, MM0           ; MACC1(0/1): copy in[n+7:n+4]    pmaddwd     MM0, [ebx+8]       ; MACC1(0/1): in[n+7:n+4] * f0[7:4]    punpckldq   MM4, MM5           ; CMPCK(2/3)PREV: unpack low out2, out3    pmaddwd     MM7, [ebx+32]      ; MACC0(0/1): in[n+3:n] * f1[3:0]    paddd       MM4, MM3           ; CMPCK(2/3)PREV: add high+low out2,out3    pmaddwd     MM1, [ebx+40]      ; MACC1(0/1): in[n+7:n+4] * f1[7:4]    packssdw    MM4, MM4           ; CMPCK(2/3)PREV: pack 32->16 out2, out3    movq        MM2, [edi+ecx+16]  ; MACC2(0/1): load in[n+11:n+8]    paddd       MM6, MM0           ; MACC1(0/1): accumulate out0    movd        [edx+ecx-4], MM4   ; CMPCK(2/3)PREV: store out2, out3    movq        MM3, MM2           ; MACC2(0/1): copy in[n+11:n+8]    movq        MM4, [edi+ecx+24]  ; MACC3(0/1): load in[n+15:n+12]    paddd       MM7, MM1           ; MACC1(0/1): accumulate out1    pmaddwd     MM2, [ebx+16]      ; MACC2(0/1): in[n+11:n+8] * f0[11:8]    movq        MM5, MM4           ; MACC3(0/1): copy in[n+15:n+12]    pmaddwd     MM4, [ebx+24]      ; MACC3(0/1): in[n+15:n+12] * f0[15:12];   ***Empty Vpipe slot***    pmaddwd     MM3, [ebx+48]      ; MACC2(0/1): in[n+11:n+8] * f1[11:8];   ***Empty Vpipe slot***    pmaddwd     MM5, [ebx+56]      ; MACC3(0/1): in[n+15:n+12] * f1[15:12]    paddd       MM6, MM2           ; MACC2(0/1): accumulate out0    movq        MM2, [edi+ecx+8]   ; MACC1(2/3): load in[n+7:n+4]    paddd       MM6, MM4           ; MACC3(0/1): accumulate out0    movq        MM4, [edi+ecx]     ; MACC0(2/3): load in[n+3:n]    paddd       MM7, MM3           ; MACC2(0/1): accumulate out1    movq        MM3, MM2           ; MACC1(2/3): copy in[n+7:n+4]    paddd       MM7, MM5           ; MACC3(0/1): accumulate out1    movq        MM5, MM4           ; MACC0(2/3): copy in[n+3:n]    movq        MM1, MM6           ; CMPCK(0/1): copy out0    pmaddwd     MM2, [ebx+72]      ; MACC1(2/3): in[n+7:n+4] * f2[7:4]    punpckhdq   MM1, MM7           ; CMPCK(0/1): unpack high out0,out1    pmaddwd     MM4, [ebx+64]      ; MACC0(2/3): in[n+3:n] * f2[3:0]    punpckldq   MM6, MM7           ; CMPCK(0/1): unpack low out0, out1    pmaddwd     MM3, [ebx+104]     ; MACC1(2/3): in[n+7:n+4] * f3[7:4]    paddd       MM6, MM1           ; CMPCK(0/1): add high+low out0,out1    pmaddwd     MM5, [ebx+96]      ; MACC0(2/3): in[n+3:n] * f3[3:0]    packssdw    MM6, MM6           ; CMPCK(0/1): pack 32->16 out0, out1    movq        MM0, [edi+ecx+16]  ; MACC2(2/3): load in[n+11:n+8]    paddd       MM4, MM2           ; MACC1(2/3): accumulate out2    movd        [edx+ecx], MM6     ; CMPCK(0/1): store out0, out1    movq